Difference between revisions of "Bicycle Gearing"
Jpferguson (talk | contribs) m |
Jpferguson (talk | contribs) m |
||
| Line 354: | Line 354: | ||
I think that the best method for doing this is by hand. Forester's ''Effective Cycling''<ref>Or at least the 1984 edition. I haven't checked the newer editions.</ref> has a wonderful example of how to do this, using some index cards, a straight-edge, some scissors and some log-scale rulers printed in the book.<ref>Why a logarithmic scale? Because on such a scale equal distances represent equal ratios, and as we've seen ratios are the important things here.</ref> I am not going to reproduce Forester's method here, for the same reason that I haven't re-implemented Sheldon Brown's gear calculator: the resource already exists. I do however want to give an idea what visualizing a shift pattern would look like, though. With that in mind I've put together some plots showing gearing on a few of my bikes.<ref>I made these plots using a program called Stata, because I use Stata for my daily work and know its syntax. There's an opportunity here for someone more computer-savvy to implement such plots using GNUplot or some such free software and to set up a web front-end...</ref> | I think that the best method for doing this is by hand. Forester's ''Effective Cycling''<ref>Or at least the 1984 edition. I haven't checked the newer editions.</ref> has a wonderful example of how to do this, using some index cards, a straight-edge, some scissors and some log-scale rulers printed in the book.<ref>Why a logarithmic scale? Because on such a scale equal distances represent equal ratios, and as we've seen ratios are the important things here.</ref> I am not going to reproduce Forester's method here, for the same reason that I haven't re-implemented Sheldon Brown's gear calculator: the resource already exists. I do however want to give an idea what visualizing a shift pattern would look like, though. With that in mind I've put together some plots showing gearing on a few of my bikes.<ref>I made these plots using a program called Stata, because I use Stata for my daily work and know its syntax. There's an opportunity here for someone more computer-savvy to implement such plots using GNUplot or some such free software and to set up a web front-end...</ref> | ||
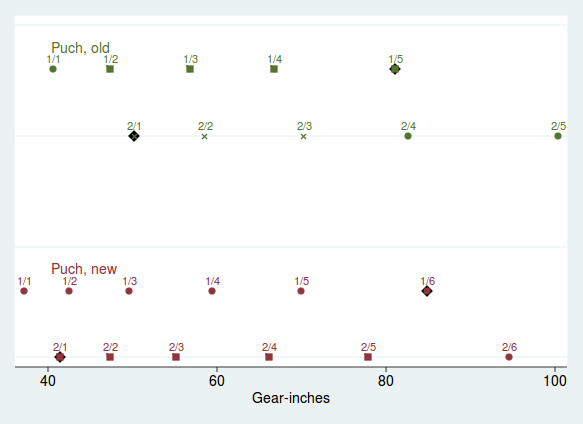
| − | [[File:puch_gears. | + | [[File:puch_gears.png|Figure 1: Old and new shifting patterns for the Puch Cavette II]] |
Figure 1 shows the old and new shifting patterns for my ten-speed. The green dots are for the old ten-speed crossover pattern; the red show the new twelve-speed half-step pattern. I have listed the "F/R" name next to each gear. The shape of the gear's marker tells you how many shifts you need to get down into it from the one above: circles are single shifts, squares are doubles and exes are triples or higher. If a gear marker has a black diamond behind it, that gear is one of the crossed ones. (These crosses aren't as serious here with rear cassettes that have fewer sprockets.) | Figure 1 shows the old and new shifting patterns for my ten-speed. The green dots are for the old ten-speed crossover pattern; the red show the new twelve-speed half-step pattern. I have listed the "F/R" name next to each gear. The shape of the gear's marker tells you how many shifts you need to get down into it from the one above: circles are single shifts, squares are doubles and exes are triples or higher. If a gear marker has a black diamond behind it, that gear is one of the crossed ones. (These crosses aren't as serious here with rear cassettes that have fewer sprockets.) | ||
| Line 362: | Line 362: | ||
The difference here may not seem drastic. I can assure you though that the reduction in the lower gear and the more even spacing throughout have helped change this particular bike from a trial to a joy to ride. The differences between these two shifting patterns are also ''meant'' to be relatively small. I was tweaking the shifting, not building a different bike. | The difference here may not seem drastic. I can assure you though that the reduction in the lower gear and the more even spacing throughout have helped change this particular bike from a trial to a joy to ride. The differences between these two shifting patterns are also ''meant'' to be relatively small. I was tweaking the shifting, not building a different bike. | ||
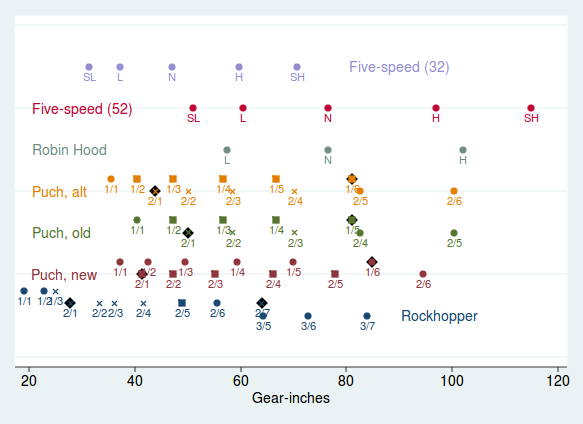
| − | [[File:bicycle_gears. | + | [[File:bicycle_gears.png|Figure 2: Shift patterns for various of my bicycles]] |
To see some more drastic differences, see figure 2. Here I have placed the Cavette II patterns from figure 1 alongside several other bicycles both built and hypothetical. Consider first the "Puch, alt" row. This is the shifting pattern that I would have had on the Cavette II if I had swapped out the old five-speed freewheel for the new six-speed but left the front sprockets unchanged. The new freewheel by itself made virtually no difference--it just added two lower gears to the pattern. Similarly changing the front sprockets while leaving the old freewheel in place would have given me the half-step pattern, more or less, but with an even ''higher'' climbing gear. It was by playing around with different visualizations like this<ref>I did the actual playing around using the paper method demonstrated in Forester's book. You could however use scatterplots like these.</ref> that I determined that I would have to change both the rear ''and'' the front sprockets on the Cavette II to get the shifting pattern that I really wanted. | To see some more drastic differences, see figure 2. Here I have placed the Cavette II patterns from figure 1 alongside several other bicycles both built and hypothetical. Consider first the "Puch, alt" row. This is the shifting pattern that I would have had on the Cavette II if I had swapped out the old five-speed freewheel for the new six-speed but left the front sprockets unchanged. The new freewheel by itself made virtually no difference--it just added two lower gears to the pattern. Similarly changing the front sprockets while leaving the old freewheel in place would have given me the half-step pattern, more or less, but with an even ''higher'' climbing gear. It was by playing around with different visualizations like this<ref>I did the actual playing around using the paper method demonstrated in Forester's book. You could however use scatterplots like these.</ref> that I determined that I would have to change both the rear ''and'' the front sprockets on the Cavette II to get the shifting pattern that I really wanted. | ||
Revision as of 10:32, 11 June 2010
Note: This page is based on notes for a talk on bicycle gearing that John-Paul Ferguson, one of the Bike Kitchen's staff, gave on 6 June 2010.
Contents
Introduction
Few things affect the "ride" of a bicycle as much as its drive train, but most cyclists never learn the details of how bicycle gearing works. People obsess about frame weight, about chain lubrication, about the height of their saddle and the length of their stem, all in pursuit of an efficient ride. Things like this play their part, but if your climbing gear is too high or you can't move easily between different gears, you'll negate much of that good work. With that in mind, I wrote this document to summarize what I know about bicycle gearing.
First, who am I? I am not a master mechanic nor a bicycle engineer. I am a sociologist, actually--but one who loves riding bikes, loves building bikes and has volunteered as a bike mechanic for several years. I have direct experience with crossover gearing, "alpine" gearing, half-step gearing and planetary gearing (fear not, I'll explain those terms below). I paid no attention to my own gears until I started taking long rides around eastern Massachusetts on a rebuilt ten-speed from the 1980s. It didn't take long to decide that the bike's lowest gear wasn't low enough for the terrain that I faced. I started reading up.
While traveling this road, I have learned two things worth stating at the beginning. First, bicycle gearing isn't that complicated. You need some arithmetic, some algebra, and some judgment. Second, there are a ton of resources out there to read up on this subject. Sheldon Brown's web site, which is a treasure-trove of information on bicycling in general, has some excellent discussion of the subjects that I am going to cover here. Brown's bicycle-gear calculator is also the best one online for figuring out your bicycle's nominal shifting pattern. John Forester's book Effective Cycling, which as of this writing is in its sixth edition, has an exceptionally clear discussion of how you calculate shift patterns and how you might compare them across bicycles. I recommend that anyone who reads this note also read those two sources at least.
What is my value added? First, this document puts everything that I've learned in one place. Second, I'm not an expert: there are some things that experts take for granted that I don't. With luck, my explanation will be clearer. Third, I'm not a fanatic: I don't think that there is one "true" gearing system. I think that it's much more important to know what you're going to be using your bike for and to gear it accordingly than to conform to someone else's idea of the "perfect" system.[1]
Terms
Some definitions. "Gears" and "sprockets" are both types of toothed wheels used in machines. Technically a gear is a toothed wheel that meshes with another toothed wheel, while a sprocket meshes with a chain. A "cog" meanwhile is a tooth on such a wheel. I mention this because bike people, like any people, like their jargon. You'll often hear people talk about "front rings" and "rear cogs" and suchlike. In this document I use the following verbiage: all the toothed wheels, front and back, are sprockets. The "gear" refers to the combination of sprockets that you're using. That is to say, "You're in your lowest gear when the chain is on the smallest front sprocket and the largest rear sprocket." I won't use "cog" because it needlessly complicates things.
I will assume that you know what the other parts of the bicycle are called, or that you can look them up.
I will often refer to "crossed" gears or a "crossed" chain. By this I mean the gears that chain together the smallest front and rear sprockets or the largest front and rear sprockets. These are the gears in which the chain is farthest from parallel with the plane of the frame. These are much less efficient gears than you might think. In addition, the small-small combination puts disproportionately large stress on all the parts of the drive train. It is good practice to avoid crossed gears on bicycles, though there are some benefits to using them in certain gearing set-ups, which I will try to mention below. As a rule, if you haven't heard a specific reason why you might want to use a crossed gear, don't. With luck, this guide will give you the knowledge you need to decide for yourself, once you have calculated and visualized a shifting pattern, whether you can ride in these gears.
Common measurements
It is impossible to talk systematically about gears without having a way to refer to them that is comparable across bicycles. That means that the beginning cyclist's "highest gear," "climbing gear" et cetera aren't going to help us. Nor for that matter will the fixed-gear fanatic's "42/15," "49/14" and the like. Five things can determine the bicycle's gear:
- The number of teeth on the front sprocket (<math>F</math>)
- The number of teeth on the rear sprocket (<math>R</math>)
- The diameter of the wheels (<math>D</math>)
- The length of the cranks (<math>C</math>)
- The teeth on the gears of an internally-geared hub, if one is present (<math>S</math>, <math>P</math>, and <math>A</math>)
All of the common measurement systems refer to some or all of these.
Gear-Inches
Gear-inch is the oldest measurement still used. It's also the most intuitive, once you know where it comes from. Where it comes from is itself kind of cool, because gear-inches are a relic of the transition from high-wheelers (the old "penny farthings" or "ordinaries") to the modern safety bicycle.
On the bicycles of the 1860s, 1870s and 1880s, the cranks were attached to the hub of the front wheel. This meant direct drive: turning the pedals once turned the front wheel once, moving the bicycle forward a distance equal to the circumference of the front wheel. The formula for the circumference of a circle is <math>D\pi</math>, and <math>\pi</math> is a constant 3.14159.... The important variable therefore is <math>D</math>, the diameter of the front wheel.
Imagine that you had a mountain bike with standard 26-inch wheels and that the cranks were attached to the front wheel. If you wanted to go twice as fast, you'd have to turn the cranks twice as fast. Alternatively, you could put a wheel that had twice the diameter on the bike. With a 52-inch wheel, then each turn of the pedals would advance the bike twice as far (because <math>(2D)\pi=2(D\pi)</math>, natch). If you pedaled at the same rate as on the 26-incher, you'd go twice as fast, though you'd be pushing rather harder. You can see why early cyclists, in the search for speed, went for big wheels in a big way.
That, at root, is the key to the gear-inch system. A gear-inch measurement of 75, say, means that you're pedaling as hard and moving as fast as you would be if you were on a high-wheeler with a 75-inch front wheel. Where does the equivalency come from? The sprockets. Go back to the mountain-bike example, with its 26-inch wheels, but now assume that the bike has a "modern" drive train. Instead of turning the wheel directly, you turn a sprocket with (let's say) 20 teeth; that sprocket is attached by a chain to another 20-tooth sprocket on the rear wheel. Because the number of teeth on the sprockets is the same, turning the pedals once will turn the rear wheel once, advancing the bike <math>26\pi</math>, just like on the direct-drive high-wheeler. You could make this bike go twice as fast by attaching a 52-inch rear wheel, but you could also do it more simply by putting a 40-tooth sprocket on the front of the bike (or a 10-tooth sprocket on the rear). Now, each turn of the pedals will still turn the front sprocket once, and the front sprocket will turn the rear sprocket twice. The drive train will therefore turn the rear wheel twice for every turn of the pedals, advancing the bike <math>2\times26\pi=52\pi</math>, exactly as though you were riding a 52-inch high-wheeler. The ratio of the front to the rear sprocket teeth multiplies the effective diameter of the wheel. Hence the formula for gear-inches is simply
<math>GI=\frac{F}{R}\times{}D</math>
We don't bother with <math>\pi</math> because it's a constant.
A side note: once you understand gear-inches, you understand why drive trains are such a bonus. Most of us can't ride a high wheeler that's larger than 60 or so inches because our legs couldn't reach the pedals while straddling the wheel. Modern road bikes though have gears that can reach 115GI or higher--and can then drop to 20GI or even lower. That flexibility, achieved by swapping sprockets rather than wheels on a single-sized frame, was at least as important as safety in the rise of the modern diamond frame.
Development
Outside the U.S., most people use the metric system. It follows that gear-inches aren't as popular. More common is to describe gears in terms of their development, which is how far down the road one turn of the pedals will advance the bike. We already know that, for a direct-drive bike, a turn of the pedals will advance the bike <math>D\pi</math>, and that a drive train modifies that distance by the ratio of the front and rear sprocket teeth. Correspondingly, the formula for development is
<math>Dev=\frac{F}{R}\times{}D\times\pi</math>
where <math>D</math> is measured in centimeters.
Gain ratio
Sheldon Brown pointed out a few years ago that neither gear-inches nor development factor in the length of the bicycle's cranks. Yet crank length matters, because the longer the cranks, the easier it is to turn a wheel of a given size, because you get the mechanical advantage of a longer lever arm. You can factor in this effect by multiplying the ratio of the sprocket teeth by the ratio of the wheel diameter to crank length, rather than by just the wheel diameter:
<math>GR=\frac{F}{R}\times\frac{D}{C}</math>
The gain ratio has the advantage that if <math>D</math> and <math>C</math> are entered in the same units then the units cancel out and the resulting number is a pure ratio. It doesn't matter whether parts are measured in inches, centimeters, or whatever; a gain ratio of, say, 3.12 means the same thing in all contexts.
Which measurement should you use?
It doesn't really matter.
I personally use gear-inches. The reason I do, to be honest, is that I'm used to gear-inches, and so those measurements have an intuitive meaning to me that the other measurements don't. I could easily use gain ratios if I put in the effort to learn the correspondences, but I am lazy.
I don't use development because I think that it's kind of stupid. I understand the need to think in metric, but that's done easily by measuring the wheel diameter in centimeters and then talking about "gear-centimeters." I think that multiplying everything by <math>\pi</math> needlessly complicates matters. Anyway, I think in inches.
Brown's point about crank-arm length is perfectly valid, and it means that two bikes that have the "same" gears measured in gear-inches or development can actually differ by the ratio of the two bikes' cranks. The thing is, crank length on 99.9% of bicycles varies within a 3% range. This means that the difference will be at most three gear-inches in the highest gear and less in the lower gears. There are applications where this is important, but all of my own bikes have cranks that are about the same size.
If I was starting from scratch I'd probably use gain ratios; feel free. I will use gear-inches elsewhere in this document, though.
What is a "good" gear?
That's up to you. People, bikes and terrain vary. What feels comfortable to me may not to you. There is no simple calculation that will tell you what single gear you want on your bike, or what range of gears. Rather, calculations like those described here help you determine which combination of sprockets, wheels and suchlike will give you the gears that you have decided are comfortable.
The classic way to figure this out is to ride several bikes, or at least one bike with several gears. When you find particular gears that you like riding in over particular terrain, take down the important measurements: note the size of the tires and count the teeth on the front and rear sprockets on which the chain is engaged. (Measure the crank arms too if you're using gain ratios.) Bear in mind what you're looking for. If you want to make the perfect single-speed, then you're looking for a gear that will get you up most of the hills you usually ride without being too pokey on the flats. If you're building a multi-speed, you have more range, but you're also looking for more things--what gear is nice on the hills, what gear keeps up with commuter traffic and so on.
This is how I end up re-gearing bikes. I already mentioned the ten-speed with the too-high climbing gear. At the other end of the spectrum, my commuter is built around an old mountain-bike frame and originally had mountain-bike gearing. I grew frustrated that I could never keep up with my girlfriend's hybrid on long rides, even though I was pedaling hard in my top gear. At the time my solution was to buy a "faster bike," the ten-speed in this case. In retrospect, I could have just changed the rear sprocket! The point is that it is hard to pick a gear from first principles but it is easy to home in on what you want based on what you're riding and how you feel about it. I'll give an example of this, based on my ten-speed, below.
Once you know the gear that you like, you reproduce it with the above equations. Say that you have a bike with 27-inch wheels and a 42-tooth front sprocket and you like riding in 75GI. Plug in 42 for <math>F</math>, 27 for <math>D</math> and 75 for <math>GI</math> in the gear-inch equation and solve for <math>R</math>. You want a 15-tooth rear sprocket.
What is a "good" set of gears?
This is easier to answer. Most of us want some common features in whatever set-up we choose:
- A high-enough high gear
- A low-enough low gear
- Reasonably even spacing between those two extremes
- A shifting pattern that is easy to remember
- Relatively few complicated shifts within that pattern
The gearing set-up that maximizes all of these features is rare; most of the common approaches trade some features off of others. Still, it is useful to know what it is you're trading!
Before we talk about shifting patterns in the abstract, it's useful to know how to calculate the shifting pattern for your bike. Bikes have <math>f\times{}r</math> gears, where <math>f</math> is the number of front sprockets and <math>r</math> is the number of rear sprockets. You can picture a table that shows all of a bike's gears, arranged by sprocket. (Sheldon Brown's gear calculator is handy here; this is what it does.) Imagine that you have a ten-speed. In fact, imagine that you have my old ten-speed: a pretty, blue-and-white Puch Cavette II from 1982. The Cavette II came with 42 and 52-tooth sprockets in front and a freewheel with 14, 17, 20, 24 and 28-tooth sprockets in the rear. It had 27-inch wheels. With that information, we can calculate its gears in gear-inches:
| 52t | 42t | |
|---|---|---|
| 28t | 50.1 | 40.5 |
| 24t | 58.5 | 47.3 |
| 20t | 70.2 | 56.7 |
| 17t | 82.6 | 66.7 |
| 14t | 100.3 | 81.0 |
To figure out the bike's shift pattern, sort the gears by gear-inches. I am going to include two other pieces of information: the percentage difference between each gear and the gear above it, and the number of shifts (moves on either sprocket) required to move down into the gear from the one above it:
| GI | % Change | Shifts | |
|---|---|---|---|
| 52/14 | 100.3 | . | . |
| 52/17 | 82.6 | 21.4 | 1 |
| 42/14 | 81.0 | 1.9 | 2 |
| 52/20 | 70.2 | 15.4 | 3 |
| 42/17 | 66.7 | 5.2 | 2 |
| 52/24 | 58.5 | 14.0 | 3 |
| 42/20 | 56.7 | 3.2 | 2 |
| 52/28 | 50.1 | 13.2 | 3 |
| 42/24 | 47.3 | 5.9 | 2 |
| 42/28 | 40.5 | 16.8 | 1 |
Notice four things about this shift pattern. First, there is a big jump between the highest and second-highest gears but almost no difference between the second- and third-highest gears. This big-jump/little-jump pattern repeats down the table. This means that the "ten" speed has fewer distinct gears--six or seven at most. Second, the big jump in the top gears means that you have few options between super-hard to pedal (100.3) and something good for mild hills (82.6). There is a "hole" in the shift pattern here. Third, the lowest gear is 40.5. That's too high a gear for me to use on long, steep climbs without feeling it in my knees, and take my word for it that I'm not especially weak. Fourth, notice how many shifts are required to move through these gears in order. To get from 81.0 to 70.2, you need to switch from the small to the large front sprocket while simultaneously moving two sprockets "down" in the back. Granted, you can make a simpler shift by going from 81.0 to 66.7, but then you're making half again as large a change while underlining that this bike doesn't really have ten gears.
There are reasons why a bike might have gears set up like this. If you mostly rode this bike on flat or moderately hilly terrain, this overall range might be fine--and the Cavette II, like a lot of ten-speeds from the 1970s/80s boom, was sold as a "road racing" bike. If you spend a lot of time fighting headwinds and little time climbing hills, you might prefer to have many closely spaced gears in the middle of your range, with one "attacking" gear at the top and a low-but-still-pretty-high gear for "powering" up the odd hill. I however am not a racer; what's more, I used to ride this bike in the hills of eastern Massachusetts and now pedal around in the Marin headlands. This is not a good set of gears for me.
With this in mind, let's address a common misconception about "fast" and "slow" bicycles. Many times I've heard someone who's starting to build a bicycle around a road-bike frame rhapsodize about how "the bigger wheels" are going to make them go so much faster. If you go back and study the formulas for measuring gears, you'll notice that most of the variation comes from the ratios of the sprockets. The difference in diameter between a road-bike tire and a mountain-bike tire is one inch or less. That means that if you go from 26- to 27-inch tires, you increase all of the gears by a whopping 4 percent. Meanwhile, switching from a mountain bike's 42-toothed "big" front sprocket to a road bike's 52-toothed one will raise all of the corresponding gears by 24 percent. This is why it is easy to build a "fast" bike for city riding around a mountain-bike frame: it's the sprockets, not the wheels, that most influence the gears.
Shift patterns
Single-front-sprocket gearing
Before moving to fancier shifting patterns, consider a bicycle that has multiple sprockets in the rear and one sprocket in the front, like the early derailer-geared British "club" cycles of the 1950s. On such a bicycle three things determine the shift pattern:
- The ratio of the front sprocket to the smallest rear sprocket gives you the high gear
- The ratio of the front sprocket to the largest rear sprocket gives you the low gear
- The ratios of adjacent rear sprockets give you the spacing between the gears
That third point is worth emphasizing. On this bike, <math>F</math> and <math>D</math> are constants. All of the differences in gears are driven by the values of <math>R</math>, the teeth on rear sprocket. This means for example that if you want five evenly spaced gears then you want as close to a constant ratio among the rear sprockets as possible. Consider a 14-17-20-24-28 five-speed sprocket. The percentage jumps from first to second, second to third and so on are 21, 18, 20 and 17 respectively.[2] You can estimate whether a rear set of sprockets has a constant ratio just by looking at it: if it looks like a cone with straight sides, then it has a pretty constant ratio.
Most rear sprocket groups are designed this way, but there are exceptions. One such is Shimano's popular "Mega-range" rear group, which has several constant-ratio gears plus a much larger low gear. The idea behind the Mega-range is that you spend most of your time riding in the higher gears but may need to drop way down to climb a steep hill, and that nice, even spacing isn't as important then.
Multiple-front-sprocket gearing
The other reason to first consider a bike with one front sprocket is so that it will be more obvious how multiple front sprockets affect a shifting pattern. Any two front sprockets have a ratio between them, just as the rear ones do. Thus shifting between two front sprockets will move all of the gears up or down by that ratio.
Consider again the Cavette II described above. Shifting from the lowest gear, 42/28, up to 42/24 is a 16.8% increase. This percentage comes from the 1.168 ratio between the 28- and 24-tooth rear sprockets. Similarly, shifting from 52/28 to 52/24 also increases the gear by 16.8%. Conversely, 52/28 is 23.8% higher than 42/28 and 52/24 is 23.8% higher than 42/24, because of the 1.238 ratio between the 52- and 42-tooth front sprockets.
One way to visualize this is to put your hands together and spread your fingers apart. The positions of your fingers represent the spacing between gears given by the ratios between the rear sprockets. Now slide the top hand back and forth, keeping the fingers splayed. The amount you slide your hand corresponds to the ratio between the front sprockets; the ratios between the rear ones stays constant. When you do this, you can for example create ten distinct gears by sliding your top hand half the distance between your fingers, such that no fingers overlap. That's "half-step" gearing, described below. You could instead slide everything so that your top index finger was between your lower middle and ring fingers. This would give you several gears clustered close together in the center, with one pinky and your thumbs hanging further away; voilà, you have "one-and-a-half-step" or "crossover" gearing, like the Cavette II that I described above. Basically, all derailer-gearing setups are characterized by how you spread your fingers and how much you slide your hands.
Below I'll discuss four gearing systems that have been used on bicycles. In these four examples I will assume that the bike has two front sprockets. I'll cover "granny gears," or third front sprockets, afterward.
Crossover gearing
Crossover gearing is the most common style found on bikes since the late 1970s . A crossover system uses constant-ratio rear sprockets and front sprockets whose ratio is larger than the ratio between the rear sprockets (Often 1.5 times larger; hence the alternate name). The idea here is to pick a general range of gears with the front sprocket and then to fine-tune things with the rear sprockets. An advantage of crossover gearing is that, because of the big jump between the front sprockets, you can get a larger overall range with any given rear sprockets. The shift pattern also isn't too complicated; you just have to learn at what point it makes sense to drop from the big to the small front sprocket and avoid crossing the chain. An important drawback of crossover gearing is that the 1.5:1 ratio can produce a lot of duplicate gears, as in the Cavette II above. This is less of a problem with modern seven-, eight- and nine-speed rear sprockets; indeed duplication can simplify the shifting pattern. On older four-, five- or six-speed rear sprockets, duplicate gears are more unappealing.
"Alpine" gearing
A true Alpine system is one like Shimano's Mega-range, where you have a range of evenly spaced cruising gears separated by a big jump from a low, climbing gear. It's more this variation from constant ratios in the rear than the ratio in the front that distinguishes an Alpine pattern: the front ratio could look like a crossover, a half-step or something else. A lot of gearing systems have thus been called "Alpine" over the years. For a long time it was common to refer to the crossover system described above as such, probably because "Alpine" sounds more hard core than "crossover."
The introduction of triple front sprockets superseded Alpine systems on many bicycles because being able to reduce the tooth count in front so drastically has a similar effect with the added benefit of a wider range of climbing gears. Note that on many custom-built Alpine systems the chain is really never intended to run on the big front and big rear sprockets, and the derailer may chatter badly if this combination is used. This is one reason why you don't see a lot of good Alpine setups sold stock on new bikes; it's easy for someone who doesn't know better to do a lot of damage by using it wrong. The Alpine idea remains a useful one though to combine with the other systems described here, especially on bikes with two front sprockets.
Half-step gearing
Half-step gearing is an older system that was designed to optimize performance given two constraints: small numbers of rear sprockets and front derailers that couldn't make big jumps. In a half-step system the ratio between the front sprockets is only half that between the rear sprockets; this means that there might be only a three- to five-tooth difference between the front sprockets. In half-step, you pick a general range of gears using the rear sprockets and then fine-tune things using the front sprockets--the opposite of the more common crossover. The advantage of half-step gearing is that it gives you evenly-spaced gears throughout the range with no duplication. For that reason it was long considered the "best" system for road bikes. It does however have two limitations. First, half-step systems employ the "crossed-chain" gears. This isn't a big deal when the rear only has four sprockets, but it becomes more of a problem as you add sprockets. As a result, a twelve-speed with with half-step gearing really should have one or two holes near the ends of its range. Second, because the front-sprocket ratio is so close, a half-step system will have a narrower overall range than a crossover system with the same rear sprockets. This is one reason why people add an Alpine sprocket or a granny gear to some half-step systems. That said, careful sprocket selection can yield a half-step system with a decent range, and on a bike with limited space between the rear dropouts it is one of the most efficient setups.
Multi-range gearing
Multi-range gearing is like an extreme crossover setup. Sheldon Brown has described these best, and I paraphrase him here: Multi-range gearing uses front sprockets that have a much wider ratio than on the rear cluster (three-step or higher). As with crossover, you choose a range with the front and then chose within the range in back; unlike crossover, the two ranges barely cross over. Thus multi-range usually involves a double or triple shift to move smoothly between the two ranges, but save for that transition the movement is in single shifts.
In a sense, multi-range is reversed Alpine, where the unusually large jump happens on the front rather than the rear sprockets. Because of the drastic size difference of the front sprockets (Brown mentions using a 50-28 pair on one bike), this system is really inefficient when the chain is crossed--the small front sprocket isn't meant to work with anything other than the two or three largest rear sprockets. Thus as with a true Alpine system, you are unlikely to find a stock bicycle set up with multi-range gearing. If however you wanted to set up a touring bike that had a large range but only two front sprockets (something that I have considered lately), then multi-range gearing could be an extremely useful setup.
Granny gears
The introduction of a third front sprocket--the smaller "granny" gear[3] found initially on mountain bikes--forced some changes in the above typology. First, the addition of a third "hand" (to go back to the hand-and-fingers metaphor for a moment) made it much easier to get a wider overall range of gears with any rear cluster. At the same time, with three chain rings it is hard to set up meaningfully large jumps between gears[4] without introducing some duplication. These modifications balance one another out--more available gears means that it can be worth sacrificing some to duplication--which helps explain the popularity of granny-gear systems.
Almost all of the systems described above can be modified by adding a granny gear. In virtually all cases it's best to ignore any duplication caused by combinations of the granny gear and the smaller rear sprockets. Instead the granny can be used to add some "bail-out" climbing gears to the shifting pattern for very steep hills. This is of course why they are used on mountain bikes, but I can say from experience that a half-step-plus-granny would come in pretty handy every now and then!
Which setup is best for me?
You know the answer, but I'll say it anyway: it depends.
I can't stress enough that you might not want to bother with any of this. My commuter is a "21-speed" with three sprockets in front and seven in back. The shifting pattern is a mess: there's lots of duplicated gears and irregular jumps between the gears in all parts of the range. Yet I haven't tweaked its gearing. Why haven't I? I don't ride that bike for very long distances (usually about five miles at a go or twenty miles max), I know the location of seven or eight useful gears within that range, mountain-bike gearing is designed with some redundancy and overlap in the gearing and life is short. I have other things to obsess about. You may feel the same.
The second that you find yourself thinking something like "I want a faster bike" or "This thing sucks for climbing," though, it's time to do your homework.
Let's go back to the ten-speed example. After two years' riding, I decided that the Cavette II had too high a climbing gear,[5] had a top gear that I only used when spinning on long descents and seemed to have many gears in the middle that weren't all that different. I therefore decided to put build a gearing system that would give me a lower bottom gear and more evenly spaced gears overall, and I wasn't that worried about losing power at the top. I decided that a half-step system might work well for me. I replaced the bike's old 14-17-20-24-28 five-speed freewheel with a 14-17-20-24-28-32 six-speed one, and I replaced the 52-42 front sprockets with 49-44 ones. The rear sprockets have a ratio around 1.20, and the front sprockets have a ratio of 1.11, giving the half step. Consider the shift pattern:
| GI | % Change | Shifts | |
|---|---|---|---|
| 49/14 | 94.5 | . | . |
| 44/14 | 84.9 | 11 | 1 |
| 49/17 | 77.8 | 9 | 2 |
| 44/17 | 69.9 | 11 | 1 |
| 49/20 | 66.2 | 6 | 2 |
| 44/20 | 59.4 | 11 | 1 |
| 49/24 | 55.1 | 8 | 2 |
| 44/24 | 49.5 | 11 | 1 |
| 49/28 | 47.3 | 5 | 2 |
| 44/28 | 42.4 | 11 | 1 |
| 49/32 | 41.3 | 3 | 2 |
| 44/32 | 37.1 | 11 | 1 |
With this gearing, the lowest gear is about 9% lower than it was--not a huge difference but a significant one. The top gear is also lower; I spin out faster on downhills, but I can also move into it more easily from the second-highest gear and thus employ it more on flats. In between, I have pretty consistent shifting; what's hidden in this chart is that I can always move 11% by switching the front sprockets or 20% by switching the rear sprocket.[6] The shifting pattern is also quite simple. You follow two rules to walk through the gears:
- To up (down) shift, first try to move the front sprocket up (down).
- If you can't move the front sprocket up (down), move the rear sprocket up (down) while moving the front sprocket down (up).
Every other gear transition is a double shift, but the shifts can be done in the right direction; that is, you can downshift one gear by dropping two gears with one shift and then rising one with another shift. Bar-end shifters or brake-shifter combos make such double shifts really easy, but because of the orderly movement you can even do it with stem or down-tube levers.
I really like this setup on this bike, but again consider the trade-offs. This bike isn't meant to take the serious hills around San Francisco; if I was going to use it often for that, I would either add a third front sprocket or go Alpine and swap the 32-tooth in the rear for a 36. If I wanted to concentrate on unalloyed speed, I would try a smaller set of rear sprockets. The point is that, once I had an idea of the range that I would be comfortable riding in, I could figure out pretty precisely what combination of gears would make me happy.
Planetary gearing
Internally geared hubs are less common and can be more expensive than derailer systems. They are also more complicated to overhaul and service. Yet they need less servicing, and if properly maintained need a full overhaul only once every few decades. Because most such hubs use a single front and rear sprocket, they can be fitted with chain guards more easily than derailer gears and are thus popular on bikes where riders are more worried about their clothing.
The Sturmey-Archer Company took out the first patent on a three-speed internally geared hub in 1902. Sturmey-Archer was bought by Raleigh in 1903 and then sold to the Taiwanese firm Sun Race in 2000. Thus some form of Sturmey-Archer hub has been sold continuously for over a century. The most common internally geared hub model in the United States is the Sturmey-Archer AW three-speed hub, which was produced and sold on bikes from the 1930s into the mid-1970s. These are cheap and easy to find used, bare or built into old bikes, and can often be restored to health just by adding some oil. Even when in worse shape, disassembly and cleaning can usually cure whatever ails them. Other companies, notably Schwinn and Shimano, released competitor hubs over the years, and Shimano, SRAM and Sturmey-Archer have each since released seven-, eight- and higher-speed models, but all such hubs work on the same principles. My experience is that very few bike mechanics know what those principles are,[7] and so I think it's worth explaining them.
We have discussed how the ratio between front and rear sprockets' tooth counts determines how many times turning the cranks will turn the rear wheel. Let's be more specific: that ratio tells us how many times turning front sprocket will turn the rear sprocket; we have assumed that one turn of the rear sprocket equals one turn of the rear wheel. The various gears[8] of an internally geared hub modify how many turns of the rear wheel a turn of the rear sprocket will produce.
Internally geared hubs do this using epicyclic gears, more simply called sun-and-planet gears. An epicycle is a cycle within a cycle. Think of the Earth going around the Sun: the Earth revolves in a circle around the Sun while rotating around its axis. With this in mind, a sun gear is a central gear around which one or planet gears move in a circle while themselves rotating. The planet gears can in turn be enclosed by a ring with inward-facing teeth, against which the planet gears mesh while also meshing with the sun gear. This ring is called an annulus, from the Latin for "little ring."[9] If this sounds confusing, I recommend the Wikipedia entry on epicyclic gearing, which includes illustrations and examples.
In epicyclic gearing systems, one of the three components will usually be fixed, another's rotation will be the input and the third's rotation will be the output. In an internally geared hub the sun gear is on the axle, which is fixed. This produces three options: the rear sprocket can turn the wheel directly; the rear sprocket can turn the annulus, which will turn the planet gears, which will turn the wheel; or the rear sprocket can turn the planet gears, which will turn the annulus, which will turn the wheel. Hence a three-speed hub.
The equations for all this are not intuitive. Trust me that, when an annulus drives planet gears, the resulting output ratio is <math>\frac{A}{S+A}</math>, where <math>A</math> is the number of teeth on the annulus and <math>S</math> is the number of teeth on the sun gear. It follows that when the planet gears drive the annulus the output ratio is reversed: <math>\frac{S+A}{A}</math>. Surprisingly, the number of teeth on the planet gears has no effect on this basic equation. These ratios enter into the standard gearing calculations multiplicatively. Thus for example the high gear of a Sturmey-Archer three-speed in gear-inches is
<math>\frac{F}{R}\times{}D\times{}\frac{S+A}{A}</math>
I own a Robin Hood (one of Raleigh's many brands) that has a 1969 AW rear hub. That bike has a 52-tooth front sprocket, an 18-tooth rear sprocket and 700C wheels (the diameter of which we'll call 26.5 for now). If you open up an AW hub (which I had to do to clean and re-oil it, since it hadn't been maintained for 39 years) and count the parts, you'll find that the sun gear has 20 teeth, the planet gears have 20 teeth and the annulus has 60 teeth. With this information you can calculate the Robin Hood's three gears:
<math> \begin{array}{llcr}
\mathrm{High:}&\frac{52}{18}\times{}26.5\times{}\frac{20+60}{60}&=&102.1\\
\mathrm{Neutral:}&\frac{52}{18}\times{}26.5&=&76.6\\
\mathrm{Low:}&\frac{52}{18}\times{}26.5\times{}\frac{60}{20+60}&=&57.4
\end{array}</math>
Weird as it sounds, "neutral" makes sense as a name for the AW's middle gear, since the others are engaged by a small metal clutch within the hub, and the epicyclic gearing system is nothing other than a transmission, albeit a mechanically powered one.
The difference between low, neutral and high gear is the output ratio from the hub. In high gear, that ratio reduces to 4/3, implying a 33.3% increase; in low it is 3/4, implying a 25% decrease. Notice where those ratios are coming from. In high gear, the rear wheel turns four times for every three turns of the sprocket, in neutral it turns once for each sprocket rotation and in low gear it turns three times for every four four turns of the sprocket. (I mention the numbers because internally geared hub manufacturers often tout their devices' "even" gear spacing. In practice that's rare. The AW doesn't have it. The ratios are symmetric, but that won't produce even spacing.)
Thence three gears; whence five, or seven? Such systems can use "stepped" planet gears, where the narrower top half has fewer teeth than the wider lower half. One half of such a gear turns against the sun gear while the other half turns against the annulus. The ratio of the tooth counts on the different steps of the planetary gear modify the effective size of the annulus, in exactly the same way that the ratio of the tooth counts on the front and rear sprockets modify the effective size of the wheel. Thus by engaging stepped rather than straight planetary gears (You need a stepped sun gear as well), the same sized annulus can be used to produce more than two different gears. For example, the high gear in Sturmey-Archer's five-speed S5 hub is
<math>\frac{F}{R}\times{}D\times{}\frac{(S+\frac{P_2}{P_1}A)}{\frac{P_2}{P_1}A}</math>
where <math>P_2</math> and <math>P_1</math> are the tooth counts of the larger and smaller steps of the planetary gears. (Notice that the planetary gears' tooth counts per se still don't matter; only their ratio does.) The sun gear that is used in neutral is also used in "super-high" and "super-low" gears, while the other step is used with the stepped planetary gears to create the intermediary high and low gears.[10] That is more detail than we need, and which step is used in which gear varies a bit by the make and model of hub. I'll simply note therefore that higher-end internally geared hubs use this same process, piling in additional steps on the sun and planet gears and even on the annulus to generate different fractional ratios of rear-sprocket-to-wheel rotation.
Comparing shifting patterns
I don't find looking at tables with percentages intuitive. If something is called a pattern, I want to see the pattern. I'd like to see the different gears spaced out, so that I can get an idea of what's going on.
I think that the best method for doing this is by hand. Forester's Effective Cycling[11] has a wonderful example of how to do this, using some index cards, a straight-edge, some scissors and some log-scale rulers printed in the book.[12] I am not going to reproduce Forester's method here, for the same reason that I haven't re-implemented Sheldon Brown's gear calculator: the resource already exists. I do however want to give an idea what visualizing a shift pattern would look like, though. With that in mind I've put together some plots showing gearing on a few of my bikes.[13]
Figure 1 shows the old and new shifting patterns for my ten-speed. The green dots are for the old ten-speed crossover pattern; the red show the new twelve-speed half-step pattern. I have listed the "F/R" name next to each gear. The shape of the gear's marker tells you how many shifts you need to get down into it from the one above: circles are single shifts, squares are doubles and exes are triples or higher. If a gear marker has a black diamond behind it, that gear is one of the crossed ones. (These crosses aren't as serious here with rear cassettes that have fewer sprockets.)
Laid out like this, you can see at a glance several distinguishing features of the old and new shifting patterns. First, the old pattern has a considerably higher top gear and a somewhat higher bottom gear. It also has several near-duplicate pairs of gears--notice how 2/4 is almost atop 1/5 and 2/2 is almost atop 1/3. The new shift pattern has more of a regular, saw-tooth pattern to it.[14] Throughout the range, a gear produced by the larger front sprocket lies midway between two gears produced by the lower sprocket; hence the half-step designation. Furthermore, for any gear in the new shifting position one of the upper or lower gears is a single shift away, and the other is only a double shift away.
The difference here may not seem drastic. I can assure you though that the reduction in the lower gear and the more even spacing throughout have helped change this particular bike from a trial to a joy to ride. The differences between these two shifting patterns are also meant to be relatively small. I was tweaking the shifting, not building a different bike.
To see some more drastic differences, see figure 2. Here I have placed the Cavette II patterns from figure 1 alongside several other bicycles both built and hypothetical. Consider first the "Puch, alt" row. This is the shifting pattern that I would have had on the Cavette II if I had swapped out the old five-speed freewheel for the new six-speed but left the front sprockets unchanged. The new freewheel by itself made virtually no difference--it just added two lower gears to the pattern. Similarly changing the front sprockets while leaving the old freewheel in place would have given me the half-step pattern, more or less, but with an even higher climbing gear. It was by playing around with different visualizations like this[15] that I determined that I would have to change both the rear and the front sprockets on the Cavette II to get the shifting pattern that I really wanted.
Consider next the gears for the Rockhopper. This is my daily commuter, which has a granny gear. As I mentioned, this is nominally a 21-speed bike, but many of those gears overlap. Rather than make the shifting pattern look messier than it is by plotting all of them, I have plotted here only the thirteen gears that you're "supposed" to use: the three produced by the big front and three smallest rear sprockets, the seven produced by the middle front and all rear sprockets and the three produced by the small front and three largest rear sprockets.[16] You can see at a glance that the Rockhopper is geared lower than the Puch; this is a bike meant for steep hills, at the cost of less oomph on flats. Even ignoring the designed-to-overlap gears, you can still see that 2/7 and 3/5 give almost exactly the same gear. Thus even if you use the crossed 2/1, this "21-speed" only has twelve real gears. You could improve on this some but not too much; instead I think the most important thing to learn with such gearing is which combinations of sprockets are meant to be used and how to step through them in your daily riding.[17] And that 19GI 1/1 is super handy in San Francisco!
The Robin Hood is my internally geared three-speed that I use at work in Palo Alto, where it's flat. Again, a glance tells you that these old three-speeds were geared really highly. I have not yet spun out in the Robin Hood's top gear, though I've gotten this bike north of 27mph on a straightaway! The internals of the hub are of course fixed, but I could modify this bike's gearing by changing the sprockets. As an example of that, consider the top two rows, which show the gears produced by an S5 hub with an 18-tooth rear sprocket and different-sized front sprockets.[18] With the 52-tooth front sprocket that many old five-speeds were sold with, such a bike would be for racing on flat terrain. Indeed, the "S" in S5 stood for "sprinter!" I don't have the strength to do much with a top gear of 117GI, and a "super-low" gear of 50GI just doesn't seem that low to me.
But what a difference a sprocket makes! The top row shows the gears produced by the same bike, with a mountain bike's 32-tooth sprocket substituted for the original. Suddenly this five-speed looks more like the Rockhopper than the Robin Hood, perfect for hauling groceries around the city, visiting friends on Potrero Hill and suchlike. A single sprocket changes the entire "ride" of the bike, yet many people would see, say, the 27-inch tires and the drop bars and write the thing off as bad for climbing hills. So--to bring things full circle--I urge you not to judge a bike by its wheels, its weight or its handlebars when deciding how it might ride. Take the measurements; do your homework; master the gears.
=Notes=- ↑ To his credit, Brown is also a "Big Tent" cyclist. Forester, at least in earlier editions of his book, leans a bit too hard on half-step gearing for all times and places.
- ↑ Because sprockets have to have whole numbers of teeth (No 15.4-tooth sprockets!), it's hard to keep the ratios exactly constant, but it's possible to keep them within a few percentage points.
- ↑ I'm breaking my promise to call these "sprockets" rather than "gears," but "granny gear" is the best-known term and "granny sprocket" sounds both weird and vaguely naughty.
- ↑ You could set up a "third-step" system, but given the common ratios found between rear sprockets such a combination would merely involve smaller gradations within the same overall range.
- ↑ I think that it's good practice on long rides to shift frequently to keep your pedaling cadence as constant as possible, whatever your speed on the road. Eventually you'll encounter a steep-enough hill that you'll have to pedal harder and slower, or even stand up; but that should be at the extreme. I reached that point too quickly and too often with a low gear of 40.5. It was this that convinced me to search for a lower climbing gear.
- ↑ Notice again that it is the ratio rather than the difference between the gears that matters. The jump between 37.1 and 41.3 feels about the same as the jump between 84.9 and 94.5, even though one moves 4.2 gear-inches and the other moves 9.6. Both are an 11% increase.
- ↑ Probably more mechanics, even professional ones, can overhaul or repair an internally geared hub than can explain how it works. Sutherland's for example has instructions for taking apart and reassembling many S-A hubs but never details how their gearing works.
- ↑ And they are gears, not sprockets, inside the hub.
- ↑ Yes, "anus" has the same root. Stop snickering.
- ↑ This obliquely helps explain why three- and five-speed hubs are more common than four- or six-speed ones. Go back to the hands and fingers. Shifting the front derailer slides the top hand over, moving all the gears up by some fixed ratio. In internally geared hubs like the S5, one shift lever moves between low, neutral and high, like a rear derailer, but the other shift lever leaves neutral unchanged, lowers the low and raises the high. Which is weird to illustrate; it's like you go from your index, middle and ring finger to your thumb, middle finger and pinky.
- ↑ Or at least the 1984 edition. I haven't checked the newer editions.
- ↑ Why a logarithmic scale? Because on such a scale equal distances represent equal ratios, and as we've seen ratios are the important things here.
- ↑ I made these plots using a program called Stata, because I use Stata for my daily work and know its syntax. There's an opportunity here for someone more computer-savvy to implement such plots using GNUplot or some such free software and to set up a web front-end...
- ↑ The "teeth" of the saw get narrower in lower gears; that's the integer-tooth problem again.
- ↑ I did the actual playing around using the paper method demonstrated in Forester's book. You could however use scatterplots like these.
- ↑ Ignore the shapes of the symbols telling you how many shifts there are between gears. Those assume that you're walking through the full gearing. In practice this bike has only two double-shifts (3/5 to 2/6 and 2/2 to 1/3). That's a hidden but big advantage of mountain-bike gearing, if you use it right.
- ↑ At this point you might notice something odd. I said that you'll almost never find stock set-ups with true alpine or multi-range gearing, because new users can do damage riding in the wrong combinations. Yet mountain-bike gears are designed with the assumption that you won't use eight of the 21 speeds, and those eight are near the middle of the shifting pattern! This is what they call a "compromise between engineering and marketing." Those overlapping gears won't lock up the drive-train, they'll just wear it out more quickly. And no bike shop will really complain about that....
- ↑ Yes, I am building a bike around an S5 hub.